Note: You are viewing this blog post without the intended style information, which may result in formatting issues.
Note: This post was written quite some time ago, but originally not published because I never could convince myself that the order insensitivity was actually useful. Publishing it now due to yet another person asking about it.
At DEFCON 22, Dan Kaminsky and I talked a little bit about something I built which he dubbed "Storybits[1]". Storybits can reversibly transform short strings of binary data into a series of words designed to produce a mental image. Order of the words does not matter, and many typos can be corrected automatically. I already had working code at the time of that talk, but since then it's just been sitting around on my computer. People have been asking about it, so I put it up on GitHub, though it's still a hacky prototype. I've thrown together a demo and written a bit about how it works.
Human brains have enormous storage capacity, but they work very differently from computers. Let's try a little experiment. I'm going to pick a random number between 0 and 213 and give you both the binary representation of that number and the word at that position in a list of common English words. I got "1101000110000" and "radius"? Which is easier to remember? They both represent the same information, but memorizing the binary would take some real effort, whereas a single word is no problem. Our memory works on "chunks" not bits.
While we've got lots of long term memory, deliberately storing anything specific in it can be a challenge. Often people use mnemonics, such as "Please Excuse My Dear Aunt Sally", to transform complicated information into a form that is easier to memorize and recall. Most often this is used to memorize lists of things, but it is possible to generalize the technique to other kinds of data.
When information is encrypted, a large number known as a key is used. The security of a key is based on the number of operations (work) that an attacker would need to do to find the correct key. For anything even remotely secure, this value is so large that it's meaningless to most people. For convenience, a log2 scale (bits) is used to talk about key security. Doubling the strength of a key adds one bit, increasing it a thousandfold adds about ten bits. For most threat models, 96 bits should be good enough[2]. We can use a trick called key stretching to make guessing up to about a million times slower, bringing that down to 76 bits. In human terms, this would be a random sequence of 23 decimal digits, 17 letters or 7 words (from a list of about 2000).
Many mnemonic systems have been proposed[3] and generating syntactically valid sentences is a really good idea, but implementation is far from trivial. Storybits is my iteration of that. Rather than actual sentences, it generates a series of adjective, noun, verb tuples. Building good wordlists for such a system is fairly tricky. I gathered up lists of common English words split up by type of speech, then filtered out words that were too long, too short or too similar[4]. Finally, Dan and I manually removed words that were semantically similar to other words, had high potential to combine offensively with other words or were hard to spell. We stopped somewhat arbitrarily at 256 words per list. Combined with some clever algorithms, we get a mnemonic passphrase system that handles typos and allows the words to be entered in any order.
How it works
Encoding
Start with an integer x in the range [0, m)[5] — cracking the encoded output will take the same amount of work as guessing x.
Example:
Select m = 220 and randomly choose x = 901713.
Run a parameter search to find the smallest number of tuples that can represent m. The result will depend on the number wordlists in use and how many words each contains. The algorithms work with any number of wordlists of arbitrary size, but any given word cannot appear in multiple lists.
Example:
Use three wordlists containing 11, 13 and 7 words respectively.
The notation nCk refers to the number of ways k items can be chosen from a list of n items[6].
11C1 × 13C1 × 7C1 = 1001 < m
11C2 × 13C2 × 7C2 = 90090 < m
11C3 × 13C3 × 7C3 = 1651650 ≥ mSo three tuples of are needed, nine words total.
Break down x into smaller ones, each corresponding to a combination of words from one of the wordlists.
Example:
t = x = 901713
11C3 = 165; c1 = t mod 165 = 153; t = t div 165 = 5464
13C3 = 286; c2 = t mod 286 = 104; t = t div 286 = 20
7C3 = 35; c3 = t mod 35 = 20; t = t div 35 = 0So c = (153, 104, 20).
Convert the combination number for each wordlist into a set of positions using a combinatorial number system.
Example:
t = c1 = 153
11C3 = 165 > t
10C3 = 120 ≤ t; p1 = 10; t = t − 120 = 33
9C2 = 36 > t
8C2 = 28 ≤ t; p2 = 8; t = t − 28 = 5
6C1 = 6 > t
5C1 = 5 ≤ t; p3 = 5; t = t − 5 = 0So p = (10, 8, 5) for this wordlist.
Words taken based on those computed positions are grouped into tuples.
A canonical string representation of those word tuples is returned as the output passphrase.
Decoding
- Start with a typed passphrase.
- The typed passphrase is converted to lowercase and any character that's not a letter or space is removed. Wherever possible typos are corrected and missing spaces are restored.
- The words are converted into sets of positions for each wordlist using lookup tables. These tables also have alternate spellings and verb tenses for many words.
- The sets of positions are turned back into a number for each wordlist by reversing the combinatorial encoding.
- Those numbers are combined back into the original integer.
Efficiency
The number of bits represented by w words from a set of n wordlists W1…Wn respectively containing |Wi| words, where w is an integer multiple of n, can be computed as follows:
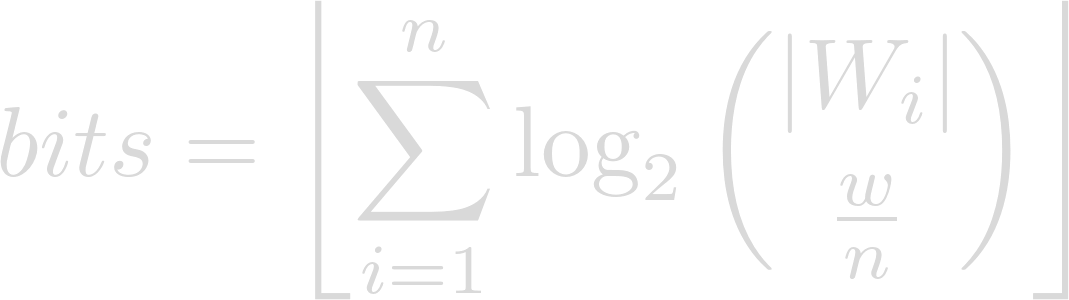
In other words, take the sum of the binary logarithms of the number of possible ways to choose w ÷ n words from each wordlist, rounding down. With the wordlists used in this demo, we get the following values:
| Words | 3 | 6 | 9 | 12 | 15 | 21 | 30 | 36 | 51 | 60 | 90 | 141 | 288 | 369 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bits | 24 | 44 | 64 | 82 | 99 | 130 | 173 | 200 | 260 | 293 | 389 | 516 | 720 | 754 |
Notice that as the number of words increases we get diminishing returns on the number of bits represented — this is the price of order insensitivity.
Demo
Try generating a random passphrase (this demo encodes 80 bits), then re-type it in the passphrase box with typos and/or words out of order. The error correction algorithms need to precompute some data structures to work effectively, which is done in the background since it takes a few seconds. There will be a message in the box at the bottom of the form when it's done. It can be used with limited error correction almost immediately. It's pretty tolerant of sloppy typing.
Full error correction can turn "amswe3rforbadcablenachoxacidrusticvfetchdjacketstuffopenhackyriot" back into "macho acid answering rustic cable fetching stuffy jacket forbidding wacky riot opening".
What's it good for?
The use cases Storybits was designed around are passphrases and public key fingerprints. It can be frustrating to type a long passphrase, especially in an application that uses key stretching, because if you make any errors, you have to type the whole thing over again. I think that error correction would go a long way towards mitigating that problem. Public key fingerprints (which also include things like Bitcoin addresses and hidden service addresses) tend to be difficult to memorize and cumbersome to type and Storybits may be helpful for that as well. I'm not ready to recommend actually using it for anything yet — the wordlists still have room for improvement and usability studies should be done — but I'm interested to hear what people think of it.
| [1] | I'm not really a fan of the name, but it'll do for now. |
| [2] | An adversary willing and able to spend the tremendous resources needed to crack a 96 bit key can probably get around the problem by rooting your box or employing rubber-hose cryptanalysis to recover it instead. |
| [3] | Mnemonic .onion URLs |
Diceware |
BIP39 |
mnemonicode |
How to memorize a Random 60-bit String If you know of any other schemes I should list here, please contact me. Things like the S/KEY and PGP wordlists are not listed because they are not designed to be used in mnemonic systems. |
| [4] | Specifically, each word has a Damerau-Levenshtine distance of at least two from every other word so that any single typo won't change one valid word into another valid word. |
| [5] | This is interval notation meaning "at least 0 but less than m". |
| [6] | Calculated using binomial coefficients. |